Hello everyone, I hope you are doing great, I am back with another blog in which I discussed a common category of problems involving trees, the problems seem tricky at first but solving these problems with the technique explained below becomes really easy.
So let's delve into the process.
You may have encountered a category of problems like
Given a pair (K, V), find the Kth ancestor of some node V in a tree.
Given a pair of nodes (a,b), find the lowest common ancestor of these nodes.
The naive approach to solving this problem is to build the edge to the parent node for each node, in this way we can always move up and store the parent for each node of the tree in a parent array like parent[node] stores the parent of the node "node".
Using the strategy explained above, let's say we have Q queries and we need to traverse N edges in the worst case when we have a skewed tree giving me an overall complexity of O(Q*N).
Let's say we have queries and the number of nodes of the order 10^5 that will give me the overall complexity of 10^5 * 10^5 i.e. 10^10, and the number of operations that a computer performs in 1s are 10^8, which will give me the time as 10^10/10^8 = 100s to execute on the extreme cases which is beyond the time limit of the online judge which is 1s.
Hence, we need to use a better technique to solve these types of problems, and here comes the binary lifting as a rescue.
So, let's see what binary lifting is.
What Binary Lifting Is?
To solve the first type of problem, we need to move K nodes up so instead of moving up one by one we move up in the powers of 2, but how? The answer is that the number K can be represented as a sum of powers of 2.

Let's say K is 7 = 0111 which is 2^2 + 2^1 + 2^0 = 4 + 2 + 1, hence, make jumps of size 4,2 and 1 to reach the Kth node starting from node V which reduces the number of jumps down to 3 from 7 and hence, the time complexity for a single query is ceil(log2(K)) which reduces the time complexity to O(Q*logN) which is far better than the previous one and it will work for the given constraints of the problem.
Implementation
To implement the above strategy we use a 2d array of dimensions N * ceil(logN) called up[N][ceil(logN)] where up[i][j] represents the 2^jth ancestor of the node i.
int M = ceil(log2(N));
int up[N][M];
Let's see the next step to fill this array, first of all, fill the array for the direct parent nodes of all the nodes of the tree.

Now, the next step is to fill the array for the remaining ancestors which are easy to calculate now, it's like if you want to find the 2^2 = 4th parent for the current node then we find the 2^1 parent for the current node say par then find the successive 2^1 parent for the node par.
for(int i=1;i<N;i++){
for(int j=1;j<M;j++){
if(up[i][j-1] != -1){
int par = up[i][j-1];
up[i][j] = up[par][j-1];
}
}
}
In this way, we prepare the up array,
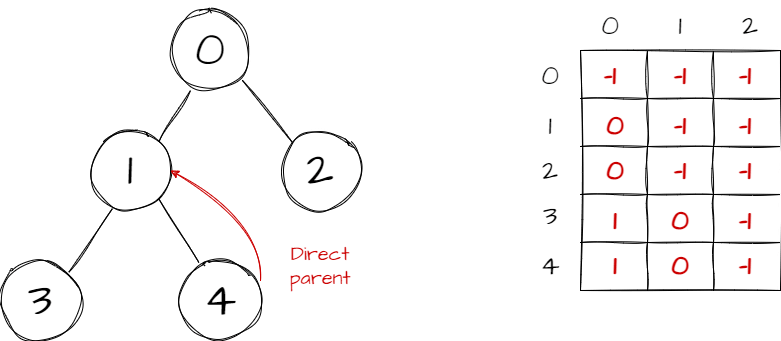
Now, Let's answer the queries using this array prepared i.e. given a pair (K, V), find the Kth ancestor of the node V, so we just need to start with the largest jump we can take from node V which is equal to the largest number which is a power of 2 and less than K which is equal to i = log2(K) and move to the node present at V = up[V][i], Now, subtract from the K the term (1 << i) i.e. 2^i, now repeat the process i.e. again find the largest power of 2 in the remaining number and keep doing until we exhaust the number.
For example: let's take K to be 7, the largest power here is 2^2 = 4 i.e. make a jump of size 4 first i.e. move from V to V = up[V][2], now subtract 4 from 7 to give 3 as the remaining number, and again find the largest power of 2 which is 2^1 and move to the node V = up[V][1] and then subtract 2 from 3 to give 1 and Now, the largest power is 2^0, and finally move to V = up[V][0] which is my answer as well.
Finally, print the answer node as V.
Let's implement the above strategy in code:
while(K){
//Find the largest power of 2
int i = log2(K);
//make a corresponding jump
node = up[node][i];
//Substract the power of 2 from K
K -= (1 << i);
}
//Print the ancestoral node
cout << node;
So, that's how we move up the tree using binary lifting :)
We need to handle an edge case here i.e. when the Kth ancestor does not exist i.e. depth of the starting node is lesser than the ancestor that we require, in that case, we shall print -1, so to handle that we need to use another array let's say level which stores the depth for each node of the tree taking root as the node at depth 0.
We know, the depth can be calculated using dfs traversal of the tree.
Let's put it all together to solve the first type of problem.
int N;
int M = ceil(log2(N));
int up[N][M];
int level[N];
vector<int>adj[N+1];
void dfs(int node, int par, int depth){
level[node] = depth;
for(auto child: adj[node]){
if(child != par){
dfs(child, node,depth+1);
}
}
}
void preprocess(){
dfs(1,0,0);
for(int i=1;i<N;i++){
for(int j=1;j<M;j++){
if(up[i][j-1] != -1){
int par = up[i][j-1];
up[i][j] = up[par][j-1];
}
}
}
}
As we have already discussed the time complexity is O(Q*logN) for the Q queries and hence for the Q and N of the order 10^5 the time will be 10^5 * log(10^5) = 10^5 which will work fine.
Problems for practice
That's all I have got for today and I hope you learned something new from this, make sure to practice the problems given in the end to get in shape so that you can "tweak" the algorithm as per the problem's requirement.
Will see you soon with something "new" :)

